How to Extract Unique Values in Excel

Andrew MossByAndrew Moss Hours
Comments 0 Comments

Extracting unique values from a range in Excel has always been possible, but not always easy. Only since the implementation of the new calculation engine has it become a doddle — thanks to the UNIQUE function.

Having said that, for many years you’ve been able to use the Remove Duplicates feature, an advanced filter or Power Query. However, nothing compares to the seamless nature of a dynamically updating formula, so that’s what I will be concentrating on.

The word unique is often abused in everyday life. Technically it means one instance of something — and only one. However, I’m sure you’ve heard someone describe something as ‘very unique’, ‘more unique’ or the ‘most unique’.

There is also another word called distinct. The two are used interchangeably by many people, yet there is a subtle difference.

Let’s just clear up what each means in data terms:

  • distinct: a value that appears at least once
  • unique: a value that appears only once

I’ve included a workbook, so please download it and follow along:

🔗 Extracting–Unique-Values.xlsb

A Microsoft 365 desktop copy of Excel is required for full functionality.

At the top is DataTable, and this contains the data used by each example. The first column (DataTable[1]) contains a full set of numbers, whereas the other (DataTable[2]) adds blank cells and errors to the mix. This has been done so you can see how the formulas respond to different scenarios.

Following this are two sections: Traditional Methods and Modern Methods. There are tables in each that have been split in half. The left side focuses on distinct values, whilst the right concentrates on unique ones.

To understand what’s behind a formula, a useful tip is to click on the argument name in the formula pop-up box and press F9. This will convert the contents to a value or array. Press Ctrl + Z to undo it.

For those running an older copy of Excel:

Aside from the modern examples (which you can’t use anyway), the traditional ones are array formulas that will only display if you press Ctrl + Shift + Return when confirming them. Microsoft 365 versions of Excel don’t require this action as they run natively.

Sorry, but I haven’t done this for you—deliberately.

Firstly, when developing the workbook, I did what worked on my version because I don’t have an older copy to test on.

Secondly, I hope seeing an error-ridden workbook convinces you to upgrade!

Traditional Methods

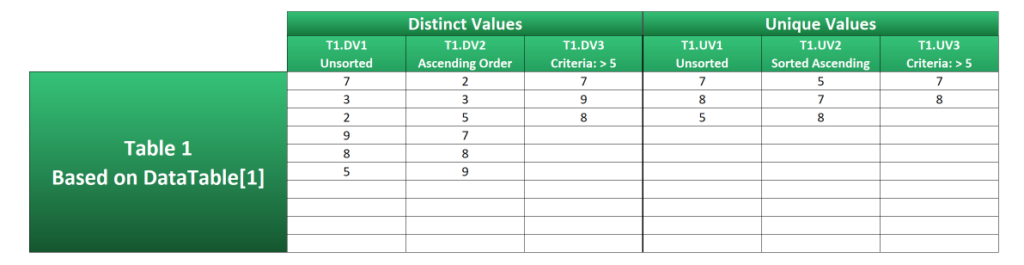
Distinct Values

Example T1.DV1 shows the most basic way of extracting distinct values from a range.

=IFNA(
INDEX(DataTable[1],
MATCH(0,
IF(DataTable[1]<>"",COUNTIF($H$23:$H23,DataTable[1]),""),
0)
),
"")

The array argument of the INDEX function references the range that the final value comes from, which is DataTable[1]. Then it’s determined which row should be returned in row_num.

MATCH(0,
IF(DataTable[1]<>"",COUNTIF($H$23:$H23,DataTable[1]),""),
0)

This part uses a combination of MATCH, IF and COUNTIF to search for the first 0 array value that the COUNTIF statement produces in lookup_array.

The range $H$23:$H23 is an expanding reference, meaning it is absolute on the left but row relative on the right. As the fill handle is dragged down from cell H24, the range will continue to start from H23 but will grow incrementally.

It always lags one cell above because only values already in the list need to be counted. In any case, you can’t reference the current cell without causing a circular reference.

When a range with multiple values is given for the criteria argument, the COUNTIF function returns multiple results in an array.

In cells H24 to H33, the COUNTIF formula converts to:

H24: COUNTIF("T1.DV1 Unsorted",{7;3;2;3;9;3;8;9;2;5})
H25: COUNTIF({"T1.DV1 Unsorted";7},{7;3;2;3;9;3;8;9;2;5})
H26: COUNTIF({"T1.DV1 Unsorted";7;3},{7;3;2;3;9;3;8;9;2;5})
H27: COUNTIF({"T1.DV1 Unsorted";7;3;2},{7;3;2;3;9;3;8;9;2;5})
H28: COUNTIF({"T1.DV1 Unsorted";7;3;2;9},{7;3;2;3;9;3;8;9;2;5})
H29: COUNTIF({"T1.DV1 Unsorted";7;3;2;9;8},{7;3;2;3;9;3;8;9;2;5})
H30: COUNTIF({"T1.DV1 Unsorted";7;3;2;9;8;5},{7;3;2;3;9;3;8;9;2;5})
H31: COUNTIF({"T1.DV1 Unsorted";7;3;2;9;8;5;""},{7;3;2;3;9;3;8;9;2;5})
H32: COUNTIF({"T1.DV1 Unsorted";7;3;2;9;8;5;"";""},{7;3;2;3;9;3;8;9;2;5})
H33: COUNTIF({"T1.DV1 Unsorted";7;3;2;9;8;5;"";"";""},{7;3;2;3;9;3;8;9;2;5})

COUNTIF will use the figures in DataTable[1] to check whether they appear in the expanding reference. If it finds a number, 1 (TRUE) is returned. If not, then it’s 0 (FALSE).

Here is what the lookup_array generates for each cell:

H24: {0;0;0;0;0;0;0;0;0;0}
H25: {1;0;0;0;0;0;1;0;0;0}
H26: {1;1;0;1;0;1;0;0;0;0}
H27: {1;1;1;1;0;1;0;0;1;0}
H28: {1;1;1;1;1;1;0;1;1;0}
H29: {1;1;1;1;1;1;1;1;1;0}
H30: {1;1;1;1;1;1;1;1;1;1}
H31: {1;1;1;1;1;1;1;1;1;1}
H32: {1;1;1;1;1;1;1;1;1;1}
H33: {1;1;1;1;1;1;1;1;1;1}

The MATCH lookup_value is 0, so the first array index with this value will be chosen. Even when numbers are repeated, this never affects the desired outcome because they will always be represented by a 1.

It’s also important to set the [match_type] to 0 for an exact match, so the formula produces the correct result.

Take cell H27 for example:

=IFNA(
INDEX({7;3;2;3;9;3;8;9;2;5},
MATCH(0,{1;1;1;1;0;1;0;0;1;0},
0)
),
"")

As the first 0 occurs in the fifth index of the array, the row_num value is 5. This means the fifth row of DataTable[1] is returned, which is 9.

IFNA has also been wrapped around the rest of the formula so all #N/A errors in non-matching cells are replaced with empty strings.

T1.DV2 sorts the same group of numbers in ascending order.

=IFERROR(
AGGREGATE(15,6,
DataTable[1]/ISNA(MATCH(DataTable[1],$I$23:$I23,0))/ISNUMBER(DataTable[1]),
1),
"")

Key to this method is the AGGREGATE function, which is often described as the ‘Swiss Army knife of Excel’ due to its versatility! It allows many types of calculations to take place, with the added benefit of having greater customisation over error handling and hidden rows.

The function_num has been set to 15, which is the SMALL function. And as 6 is stated for options, error values will be ignored.

Housed in the array argument is a conditional statement that ensures DataTable[1] is filtered correctly. The calculation starts with the range first, and then two conditions are included— each separated by a division symbol (‘/’).

The first condition checks for #N/A! errors in the MATCH statement, which evaluates each value in DataTable[1] to determine if it has already appeared in the expanding range. If so, the first instance of that number’s position is returned. If not, an #N/A! error occurs.

Formula
MATCH(DataTable[1],$I$23:$I28,0)

DataTable[1]
{7;3;2;3;9;3;8;9;2;5}

Expanding range
{"T1.DV2 Ascending Order";2;3;5;7;8}

Position of DataTable[1] value in expanding range
{5;3;2;3;#N/A;3;6;#N/A;2;4}

Cell is #N/A!
{FALSE;FALSE;FALSE;FALSE;TRUE;FALSE;FALSE;TRUE;FALSE;FALSE}

In the second condition, the ISNUMBER statement does a simple check of DataTable[1] to verify each cell contains a number.

Formula
ISNUMBER(DataTable[1])

DataTable[1]
{7;3;2;3;9;3;8;9;2;5}

Cell contains a number
{TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE}

Both conditions produce an array of TRUE and FALSE values, but for a successful calculation to take place, the same array index for each must be TRUE. The TRUE and FALSE values will automatically coerce into 1s and 0s — and dividing anything by 0 returns a #DIV/0! error.

This is how the array argument calculates for the first three cells:

I24:

Formula
DataTable[1]
/
ISNA(MATCH(DataTable[1],$I$23:$I23,0))
/
ISNUMBER(DataTable[1])

DataTable[1]
{7;3;2;3;9;3;8;9;2;5}
/
MATCH statement equals #N/A!{TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE}
/
Cell contains a number
{TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE}
=
{7;3;2;3;9;3;8;9;2;5}

I25:

Formula
DataTable[1]
/
ISNA(MATCH(DataTable[1],$I$23:$I24,0))
/
ISNUMBER(DataTable[1])

DataTable[1]
{7;3;2;3;9;3;8;9;2;5}
/
MATCH statement equals #N/A!
{TRUE;TRUE;FALSE;TRUE;TRUE;TRUE;TRUE;TRUE;FALSE;TRUE}
/
Cell contains a number
{TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE}
=
{7;3;#DIV/0!;3;9;3;8;9;#DIV/0!;5}

I26:

Formula
DataTable[1]
/
ISNA(MATCH(DataTable[1],$I$23:$I25,0))
/
ISNUMBER(DataTable[1])

DataTable[1]
{7;3;2;3;9;3;8;9;2;5}
/
MATCH statement equals #N/A!
{TRUE;FALSE;FALSE;FALSE;TRUE;FALSE;TRUE;TRUE;FALSE;TRUE}
/
Cell contains a number
{TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE;TRUE}
=
{7;#DIV/0!;#DIV/0!;#DIV/0!;9;#DIV/0!;8;9;#DIV/0!;5}

The final argument of the AGGREGATE function is [k], and this has been set to 1 so the smallest value is extracted from array.

To conclude the formula, IFERROR’s value_if_error argument returns a blank string for the redundant cells. ISNA couldn’t be used again as it does not detect #NUM! errors.

T1.DV3 is similar to T1.DV1, except it will only extract distinct values that are greater than 5. It does this due to a small change in the IF logical_test argument.

=IFNA(
INDEX(DataTable[1],
MATCH(0,
IF(DataTable[1]>5,COUNTIF($J$23:$J23,DataTable[1]),""),
0)
),
"")

Unique Values

Unfortunately, extracting unique values isn’t a simple case of making minor alterations to the formulas you’ve just seen.

Proof of this is shown in T1.UV1, where a more complex formula is required compared to its distinct equivalent in T1.DV1.

=IFERROR(
INDEX(DataTable[1],
SMALL(
IF(FREQUENCY(IFERROR(MATCH(DataTable[1],DataTable[1],0),""),
ROW(DataTable[1])-ROW(DataTable[[#Headers],[1]]))=1,
ROW(DataTable[1])-ROW(DataTable[[#Headers],[1]])),
ROWS($K$24:$K24))
),
"")

Let’s focus on the array argument of the SMALL function.

Nested inside an IF statement is the FREQUENCY function, which allows data to be grouped through ‘binning’.

It has two arguments:

data_array: generates an array specifying the first-row instance of each value in DataTable[1]. In other words, repeated numbers have the same value as their first occurrence.

FREQUENCY data_array

Formula
IFERROR(MATCH(DataTable[1],DataTable[1],0),"")

Result
{1;2;3;2;5;2;7;5;3;10}

bins_array: subtracting the heading row from the whole of DataTable[1] produces an array that is the same size as the range itself. These are the 10 bins that house the data_array indexes.

FREQUENCY bins_array

Formula
ROW(DataTable[1])-ROW(DataTable[[#Headers],[1]])

Result
{1;2;3;4;5;6;7;8;9;10}

When the two arguments are put together, the FREQUENCY statement will dump each data_array index into a matching bin in bins_array. Then, bins_array is checked for bins that contain a single value. As these are 1, 7 and 10, their respective indexes are declared TRUE.

IF logical_test
FREQUENCY({1;2;3;2;5;2;7;5;3;10},{1;2;3;4;5;6;7;8;9;10})=1

Bin has one value only
{TRUE;FALSE;FALSE;FALSE;FALSE;FALSE;TRUE;FALSE;FALSE;TRUE;FALSE}

The [value_if_true] argument then converts these TRUE values into row numbers, whilst the others remain FALSE.

IF [value_if_true]
{1;FALSE;FALSE;FALSE;FALSE;FALSE;7;FALSE;FALSE;10;FALSE}

Finally, the expanding reference ROWS($K$24:$K24) in the k argument ensures that each calculation will return the next smallest row number. Once this figure exceeds the quantity of array values, a #NUM! error occurs. However, the IFERROR function traps this and replaces it with an empty string.

Using the row numbers 1, 7 and 10 generated by the INDEX row_num argument, the values extracted from DataTable[1] are 7, 8, and 5, respectively.

T1.UV2 employs a similar method to the previous example, but it’s actually a shorter formula because the numbers are sorted in ascending order. There’s no need for the INDEX function, as SMALL takes care of the ordering.

=IFERROR(
SMALL(
IF(FREQUENCY(IFERROR(MATCH(DataTable[1],DataTable[1],0),""),
ROW(DataTable[1])-ROW(DataTable[[#Headers],[1]]))=1,
DataTable[1]),
ROWS($L$24:$L24)),
"")

T1.UV3 returns unique values greater than 5.

The formula’s MATCH statement is structured a little differently from what’s found in T1.DV3. This time the IF function does not get used—replaced by a COUNTIFS statement instead that’s added to the original COUNTIF.

=IFNA(
INDEX(DataTable[1],
MATCH(0,
COUNTIF($M$23:$M23,DataTable[1])
+
(COUNTIFS(DataTable[1],DataTable[1],DataTable[1],">5")<>1),0)),
"")

As described earlier, the first COUNTIF statement uses the values in the expanding range and searches for them in DataTable[1]. Where a match is found, its array index becomes 1.

Added to this is a COUNTIFS statement, which is necessary to allow for two conditions. The criteria_range1 and criteria1 arguments both contain DataTable[1], as this will force the function to produce an array instead of a single value. After this, the second condition ensures only numbers over 5 are checked in DataTable[1].

An array is produced from this with the total count for each: {1;0;0;0;2;0;1;2;0;0}.

Affixing <>1 to the end of the statement converts this array into a set of TRUE and FALSE values: {FALSE;TRUE;TRUE;TRUE;TRUE;TRUE;FALSE;TRUE;TRUE;TRUE}.

When the contents of lookup_array is summed, another array is formed comprising the totals of the two parts: {0;1;1;1;1;1;0;1;1;1}.

What the statement is looking for is 0, as this is the sum of two FALSE values.

M24:

Values in both expanding range and DataTable[1]
COUNTIF($M$23:$M23,DataTable[1])
{0;0;0;0;0;0;0;0;0;0}
+
Values over 5 in DataTable[1]
COUNTIFS(DataTable[1],DataTable[1],DataTable[1],">5"
{1;0;0;0;2;0;1;2;0;0}
Counts not equal to 1 (<>1)
{FALSE;TRUE;TRUE;TRUE;TRUE;TRUE;FALSE;TRUE;TRUE;TRUE}
=
{0;1;1;1;1;1;0;1;1;1}

M25:

Values in both expanding range and DataTable[1]
COUNTIF($M$23:$M24,DataTable[1])
{1;0;0;0;0;0;0;0;0;0}
+
Values over 5 in DataTable[1]
COUNTIFS(DataTable[1],DataTable[1],DataTable[1],">5"
{1;0;0;0;2;0;1;2;0;0}
Counts not equal to 1 (<>1)
{FALSE;TRUE;TRUE;TRUE;TRUE;TRUE;FALSE;TRUE;TRUE;TRUE}
=
{1;1;1;1;1;1;0;1;1;1}

The first 0 is picked out from the array and becomes the value of row_num, allowing the correct number from DataTable[1] to be returned.

M24: MATCH(0,{0;1;1;1;1;1;0;1;1;1} = row 1 of DataTable[1] = 7
M25: MATCH(0,{1;1;1;1;1;1;0;1;1;1} = row 7 of DataTable[1] = 8

Empty cells result in a clean sweep of ones: {1;1;1;1;1;1;1;1;1;1}. These produce #N/A! errors, which IFNA’s value_if_na argument cleans up with blank strings.

Handling Blanks and Errors

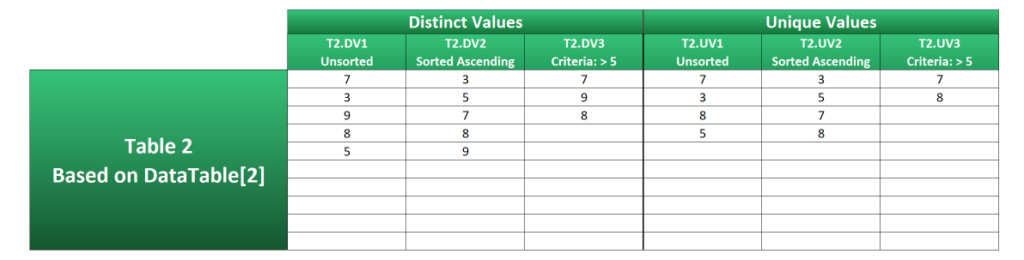
Before I move on to the modern methods, I wanted to show you how these formulas respond when there are blank cells and errors in the source data.

Table 2 makes use of the same formulas as Table 1, except it’s based on DataTable[2]. As you can see, the results are as clean as Table 1.

Modern Methods

Firstly, make yourself fully aware of the UNIQUE function given its prominence throughout this section.

Syntax

=UNIQUE (array, [by_col], [exactly_once])

Arguments

  • array: range to extract unique values from.
  • [by_col] (optional; default is FALSE): determines whether column values should be returned instead of rows. By default, rows are returned.
  • [exactly_once] (optional; default is FALSE): determines whether unique values should be returned. By default, distinct values are returned.

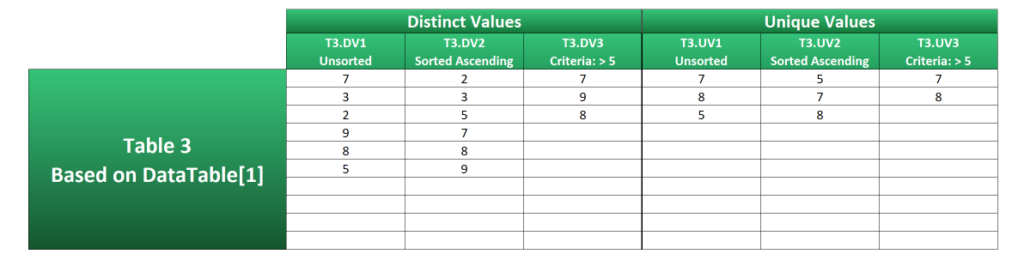
T3.DV1 demonstrates the most basic use of the UNIQUE function. The range DataTable[1] has been referenced in the array argument and the distinct values spill down from cell H24.

=UNIQUE(DataTable[1])
{7;3;2;9;8;5}

T3.DV2 builds on this by wrapping the SORT function around the original formula. This will place the numbers in ascending order. Use -1 in the [sort_order] argument for descending order.

=SORT(UNIQUE(DataTable[1]))
{2;3;5;7;8;9}

T3.DV3 shows how distinct values over 5 are extracted by wrapping a FILTER statement inside the UNIQUE function and using the condition DataTable[1]>5 in the include argument.

=UNIQUE(FILTER(DataTable[1],DataTable[1]>5))
{7;9;8}

Examples T3.UV1, T3.UV3 and T3.UV3 are constructed very similarly, except they extract unique values instead. This is done by setting the [exactly_once] arguments to TRUE.

K52:

=UNIQUE(DataTable[1],,TRUE)
{7;8;5}

L52:

=SORT(UNIQUE(DataTable[1],,TRUE))
{5;7;8}

M52:

=UNIQUE(FILTER(DataTable[1],DataTable[1]>5),,TRUE)
{7;8}

Handling Blanks and Errors

That was all straightforward, wasn’t it? Certainly compared to the traditional methods anyway. However, as shown in Table 4—which is based on DataTable[2]—these methods don’t ignore blank cells and error values. Blanks are counted as 0, and the #N/A and #DIV/0! errors are considered values in their own right.

Although the others still return a result, examples T4.DV3 and T4.UV3 completely break down because of the error values in the data. Even if you take out the #N/A from DataTable[2], the result will be #DIV/0! instead.

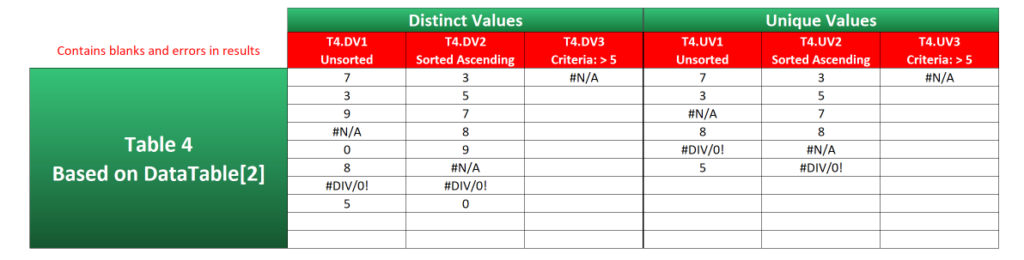
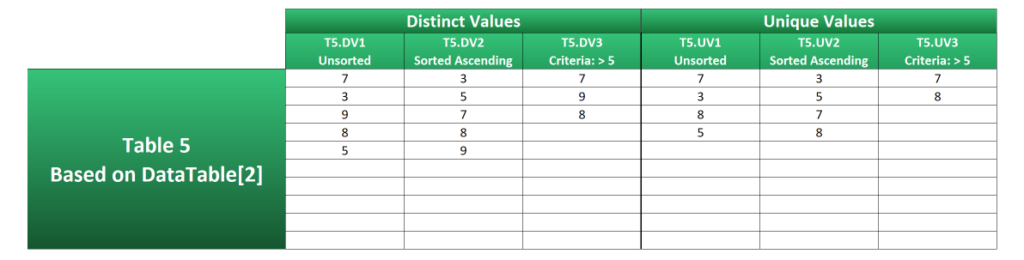
Table 5 corrects these by extending the formulas to strip out errors and blanks.

All six examples feature this additional statement in the include argument of the FILTER function:

NOT(ISBLANK(DataTable[2]))*NOT(ISERROR(DataTable[2]))

For the first part, FALSE is returned for the empty cells. The ISBLANK function itself will return TRUE, but as it’s nested in NOT, the opposite occurs. This is necessary as the include argument requires TRUE values for inclusion.

NOT(ISBLANK(DataTable[2]))
{TRUE;TRUE;TRUE;TRUE;TRUE;FALSE;TRUE;FALSE;TRUE;TRUE}

The asterisk (*) represents AND logic and allows a new condition to be introduced.

This statement returns FALSE for the #N/A! and #DIV/0! errors:

NOT(ISERROR(DataTable[2])){TRUE;TRUE;TRUE;FALSE;TRUE;TRUE;TRUE;TRUE;FALSE;TRUE}

Examples T5.DV3 and T5.UV3 have an additional FILTER statement to weed out the errors and blanks. Whilst this could be done with just one, it would involve repeating part of the formula.

The LET function allows names to be defined and assigned values. These variables can then be used multiple times in the same formula. This is great for constructing more readable formulas and reducing processing time.

Let’s focus on T5.DV3:

=LET(FilterBlanksandErrors,

UNIQUE(
FILTER(DataTable[2],
NOT(ISBLANK(DataTable[2]))*NOT(ISERROR(DataTable[2]))
)),

FILTER(FilterBlanksandErrors,FilterBlanksandErrors>5))

The formula opens with LET, and inside it the name1 argument contains the name of the value: ‘BlanksAndErrorsRemoved’.

Next, the calculation is defined in name_value1. This consists of the UNIQUE function encompassing a FILTER statement that removes blanks and errors from the range.

UNIQUE(
FILTER(DataTable[2],
NOT(ISBLANK(DataTable[2]))*NOT(ISERROR(DataTable[2]))
))

The argument calculation_or_name2 houses the second FILTER condition, but inside—the defined name is referenced instead.

FILTER(BlanksAndErrorsRemoved,BlanksAndErrorsRemoved>5)
{7;9;8}

Before the advent of the LET function, you had to repeat part of the formula to achieve this. No longer!

Final Words

When I started this article, the original plan was to show you only the modern techniques to extract unique values from a range. Then I had an epiphany.

I was driven by a desire to convince those struggling with their antiquated versions of Excel to upgrade to Microsoft 365. By demonstrating the traditional methods as well, it knew it would enable you to gain a sense of perspective—to show you how far Excel has come in a short period.

If you don’t have Microsoft 365, you cannot enjoy the pleasure of creating these new kinds of formulas. You are resigned to the clunky, cumbersome, and archaic approaches. It’s like running through treacle: you work your arse off, but the progress you make is never representative of your effort.

Even if you construct a formula that mimics a modern one, I can bet my bottom dollar that—not only has it taken you considerably longer—but it’s bound to cause issues further down the line.

When I was tinkering with the traditional formulas, sometimes I would forget to double-press the fill handle on the first cell to update the others as well. I think it must be my mind that is so accustomed to a dynamic array way of thinking.

This is a classic error people make anyway. Thankfully, in modern Excel it isn’t a problem. The one formula = many cells approach mitigates the risk of making these kinds of mistakes.

If you’re not dynamic array-ready and still using formulaic approaches of the 1990s, it’s time to change…or get left behind.

Andrew Moss

Excel Aficionado

Andrew is a technical writer who specialises in Excel and data analysis. He has published hundreds of articles and social media posts aimed at helping people enhance their skills and spreading good practices.

Subscribe
Notify of
guest

0 Comments
Oldest
Newest Most Voted
Inline Feedbacks
View all comments